Unevenness and Coefficient of Variation of Yarn

Md Sohanur Rahman Sobuj



Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018
Unevenness and Coefficient of Variation of Yarn
Yarn Evenness-1 Yarn Evenness-2 Yarn Evenness-3 Yarn Evenness-4
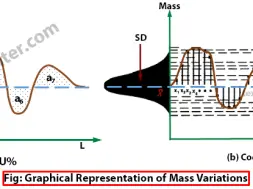
Mathematical Expression of Yarn Irregularity or Mass Variation
Generally two parameters are used to express the irregularity of yarns. They are…
- 1. Percentage of mean deviation (PMD) or Unevenness (U%)
- 2. Coefficient of variation CV%
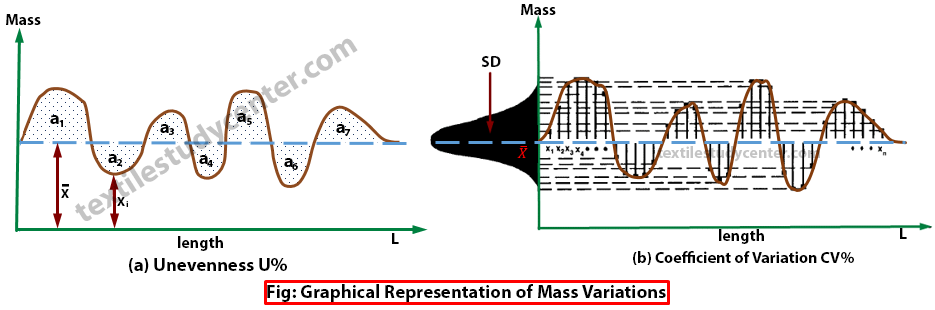
Percentage of Mean Deviation (PMD) or Unevenness (U%)
The average value for all the deviations from the mean which is expressed as a percentage of the overall mean is called percentage of Mean Deviation (PMD). This is termed Um% by the Uster Company.
Coefficient of mass Variation (CV%):
The coefficient of mass variation CV % is the ratio of standard deviation of mass variation divided by average mass variation.The higher the CV value is the more irregular the yarn.

A modern instrument, such as the Uster Evenness Tester, can measure the U and CV values of a fiber assembly at a high speed. The larger deviations from the mean value are much more intensively taken into consideration in the calculation of CV% rather than in U% (due to the squaring of the term). For this reason, the Coefficient of Variation CV% has received more recognition in
modern statistics than the irregularity value U%.


Relation between Percentage of Mean Deviation (PMD) and Coefficient of Variation CV%
If the fiber assembly required to be tested in normally distributed with respect to the mass variation, then the two parameters of irregularity are related by the following equation:

| Type of Fiber Assembly | Conversion Factor |
|
►Normal Distribution (contains purely random variations, symmetrical) ►Asymmetrical Distribution, periodic and random variations present (faulty test material e.g. with long wavelength count variations, thick places, etc.) ►Symmetric Distribution with strong periodic variations |
1.25
<1.25 viagraforhealthyman |
(8843)

Md Sohanur Rahman Sobuj



Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018