Torsional Properties of Textile Materials
Torsional Properties of Textile Materials
Torsional Property:
Fibers are twisted to form yarns, while are made into textile fabrics or ropes. The torsional properties determine how fibers respond while being twisted.
Torsional Rigidity:
The torsional rigidity is the resistance of a fiber to twisting. In the Hookean region of small stains, the torsional rigidity defined as the torque required to produce a unit twist per unit length.
[Or, as the torque to produce a unit twist in radians per unit length, when it will equal (εnc2/2πρ)]

Proof:
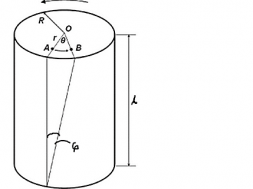
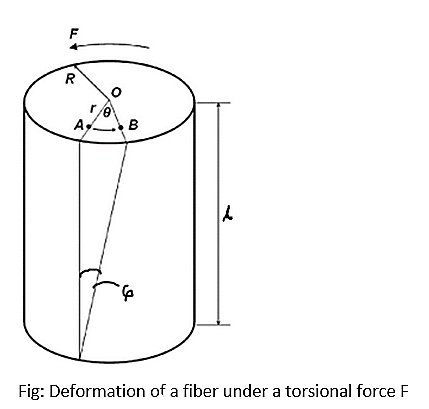
Fig. shows the de-formation of a fiber under a torsional force (F). After the fiber is twisted through an angleq, line OA on the cross-section of the fiber is displaced to a new position OB. Point O is the center of the fiber cross-section. Consider an element of area δA at a distance r from the center.


Now,

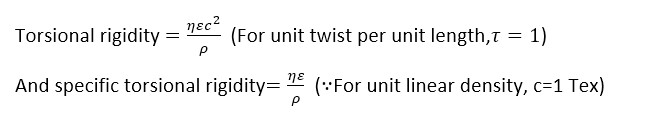
Specific Torsional Rigidity:
Specific torsional rigidity can be defined as the torsional rigidity of a fiber of unit linear density(c=1).

Shear Modulus :
Shear modulus is defined as the ratio of shear stress & shear strain. Shear modulus is measured in radians.
Breaking Twist :
The twist for which a fiber will break is called breaking twist. The breaking twist may also be defined as the number of turns that required to rupture a fiber. The number of turns to rupture is inversely proportional to the fiber diameter. If diameter of a fiber is d, then
Breaking twist, tb∞ 1/D
Breaking Twist Angle (BTA) :
Breaking twist of a fiber occurs the surface is stained into a critical angle of shear. This is called as breaking twist angle. When the breaking twist angle is less, the fiber is said to be more flexible.
The breaking twist angle (BTA) is calculated by the following formula:
Breaking twist angle (BTA) a=tan-1(pDtb)
Where, D = diameter of fiber
tb = breaking TPI
Breaking Twist Angle of Different Fiber:
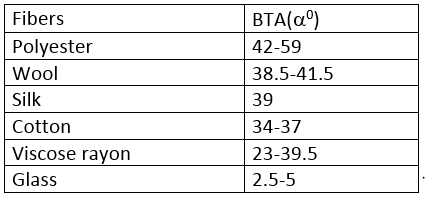
Mathematical Problem:
Breaking twist angle (BTA) a=tan-1(pDtb)
Where, D = diameter of fiber
tb = breaking TPI
Problem 01 of Torsional Rigidity :
Find out breaking twist angle of a cotton fiber, which contains 42 breaking TPI and its diameter is 0.1 mm.

Problem 02 of Torsional Rigidity :
Find out TPI (twist per inch) of yarn, where dia of yarn is 0.15 mm and breaking twist angle 35o.
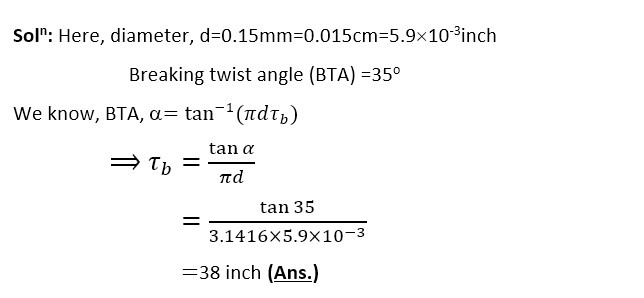
(1857)