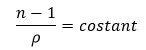
Birefringence | Fiber Birefringence
Md Sohanur Rahman Sobuj
Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018
Part 1: Optical Properties of Textile Fibers
Part 2: Birefringence | Fiber Birefringence
Birefringence | Fiber Birefringence
Birefringence
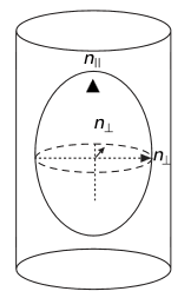
Most oriented fiber can be characterized by two principle refractive indices one parallel to the fiber axis (nιι) and another perpendicular to the fiber axis (n⊥). Here, the subscripts indicates the vibration direction of light waves.
Fig: Principle refractive indices of fiber
So, the difference between the refractive index indices of the fiber in a direction at parallel to the fiber axis and in a direction at right angles to the fiber axis is called birefringence of that fiber. Birefringence is responsible the phenomenon of double reflection.
Birefringence(Δn) = nιι-n⊥
Where, nιι& n⊥ are the refractive indices in a direction at parallel and perpendicular to the fiber axis respectively.
When fiber molecules are parallel to the fiber axis, then the fiber is more electron polarized.
∴Electron polarization↑→ Vfiber ↓→ n ↑→Birefringence ↑
Birefringence property depends on the following factors
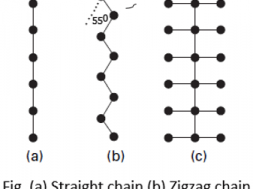
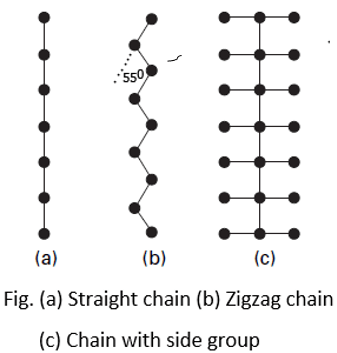
The magnitude of the birefringence depends on two factors: the degree of orientation of the molecules and the degree of asymmetry of the molecules themselves. If all the atoms in a molecule are arranged in a straight chain Fig. (a), the bond polarisabilities are greatest along the line joining the atoms, then a high birefringence will be expected. However, the actual molecules in fibers do not have this form and their birefringence will be reduced for two reasons.
⦿ Firstly, most main chains have a zigzag form Fig. (b) provided that the bonds diverge from the main axis by less than about 55°, this still gives a positive birefringence. Example, the value of the birefringence of polyester fiber is 0.188.
⦿ Secondly, there will be side groups attached to the main chain, as in Fig. (c), and these will have the effect of providing atomic bonds at right angles to the main axis. This will increase the value of n⊥ and reduce the birefringence. In triacetate and acrylic fibers, the side groups have a greater effect than the main chain, and the birefringence is negative. Example, the value of the birefringence of triacetate fiber is -0.005.
Measurement of birefringence
The measurement of birefringence is an important method for studying the molecular orientation in polymer fibers. Because, both the refractive index and birefringence of fibers change with increase in molecular orientation.
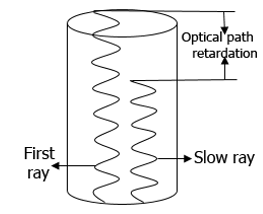
The birefringence of a fiber can be measured by directly, by determining the retardation or difference in optical path length. Science the optical path length equals the product of the refractive index and the thickness of specimen through which the light passes.
So, optical path retardation = (N +δN)λ
= (nιι-n⊥)×t
= Birefringence × Thickness
Where,
λ = wave length
N +δN = total number of wavelengths
nιι = refractive index for light polarized parallel to the fiber axis
n⊥ = refractive index for light polarized perpendicular to the fiber axis
Note1: Total no of weave length=no. of full wave (N) + no. of frictional wave (δN)
Note2: Birefringence may also be determined by measuring the retardation with the corresponding thickness of the fiber and calculated with the following formula:
Why is birefringence so important in fiber science?
When fibers absorb a large amount of moisture, water molecules mainly enter the amorphous phase and change its refractive angle. Therefore, in wet fibers, the refractive index difference between the crystalline and amorphous phase become larger and the form of birefringence starts to make contribution to the total fiber birefringence. The effect of from birefringence become significant only when the moisture regain is greater than 15%.
Optical orientation factor is generally defined as the average angle of inclination of the chain molecules in the crystalline regions with respect of fiber axis. Mathematically,
f= 0.5[3cos2θ-1]
Where
θ = angle between the elongation direction and main optical axis.
Here,
f = 1.0 for maximum parallel orientation (θ=0)
f = -0.5 for maximum perpendicular orientation (θ=90)
f = 0 for random orientation
The birefringence values can be related to optical orientation factor or the average angle of orientation of the molecule.
Where,
f = optical orientation factor
Δn = birefringence of the experimental sample
Δn’ = birefringence value of a perfectly oriented specimen
θ = average angle of orientation of the chain molecules
Relation among refractive index, density and swelling
The refractive index of fibers is affected by the fiber density. For many fibers, the relationship between refractive index and fiber density (ρ) can be expressed by Gladstone and Dale’s law:
If the average reflective index is used, the value of constant is 0.3570.
A similar relationship can be obtained between the refractive index (nm) and volume vm of a mixture of different components.
Vm(nm-1) = v1(n1-1) + v2(n2-1) + v3(n3-1) +… … … …
Where v1, v2, v3, … and n1, n2, n3, … are the reflective indices and volumes of the individual components. The refractive index of water is 1.333. So that, the effect of moisture on the refractive index can be described by:
vMR(nMR-1) = v0(n0-1) + 0.333MR
Where,
v0 = volume of 1 gm of dry fiber
vMR = volume of sample fiber at a frictional moisture reign of MR
n0 = refractive index of dry fiber
nMR = refractive index of moisture fiber
The equation applies to the refractive index nιι & n⊥ and we find how the birefringence varies with the moisture vs swelling of the fibers:
vMR( nιι – n⊥)MR = V0( nιι – n⊥)
(3093)
Md Sohanur Rahman Sobuj
Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018
