Optical Properties of Textile Fibers
Md Sohanur Rahman Sobuj
Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018
Optical Properties of Textile Fibers
When light falls on a fiber, it may be partly transmitted, absorbed or reflected, depending on the structure of the light. The transmission, reflection and absorption of light determine the visual appearance of an individual fiber. So, visual appearance of any fiber depends on the optical properties of fiber.
Polarization and light
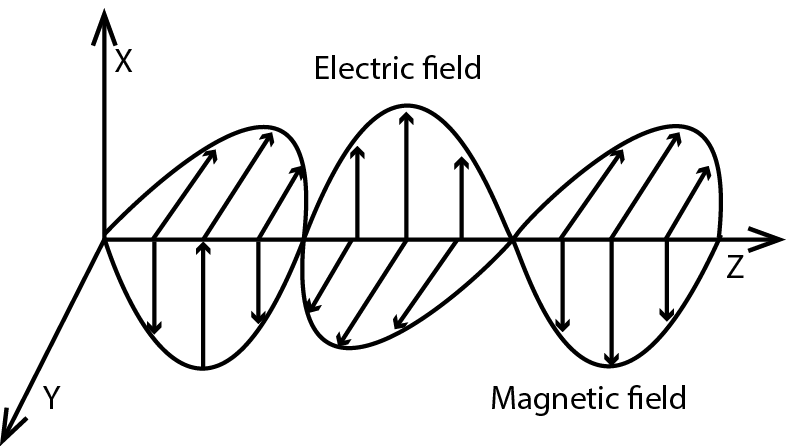
Light is an electro magnetite wave and unpolarized light. When light travels, it is distributed in two ways such as electric field and magnetic field.
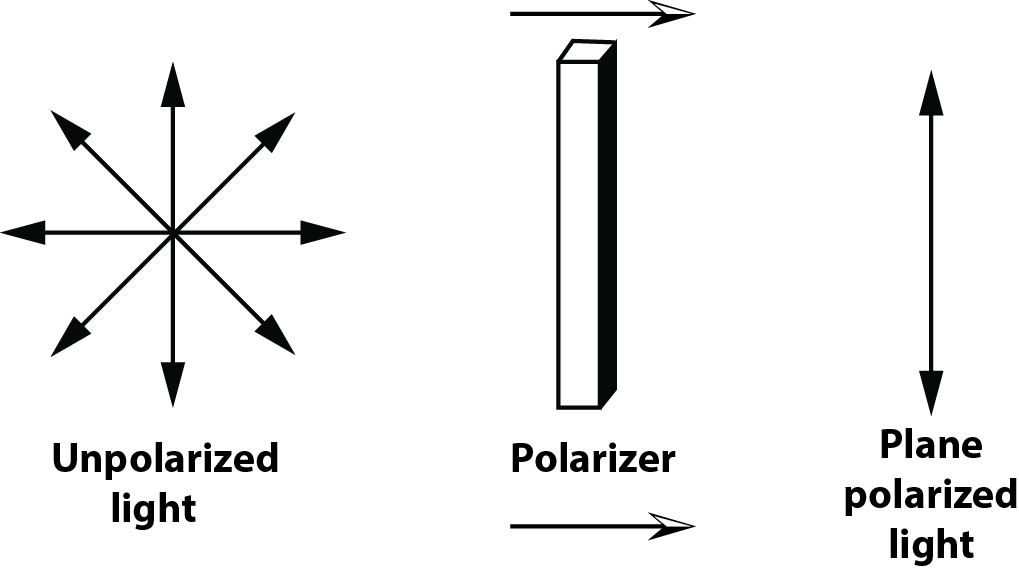
The process of transforming unpolarized light into polarized light is known as polarization. Polarized light has its E field in one direction.
Double refraction
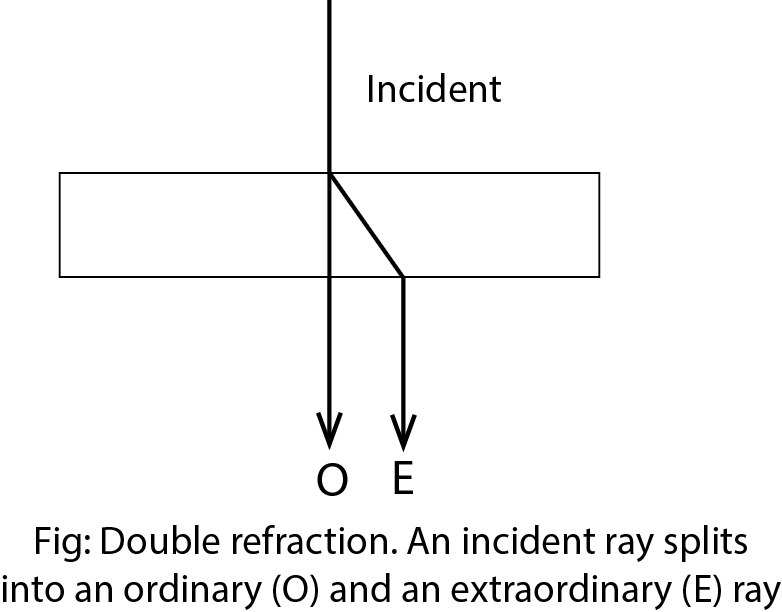
Double refraction is the property of particular crystals that allows them to split an unpolarized ray into two rays that are plane polarized light at right angles to each other. The different colors as result of double refraction.
O-ray & E-ray
For double refraction, one ray of vibration will realize a higher refractive index and refract according to Snell’s law. This is called the Ordinary ray or O-ray. Another ray, vibrating at right angles to the O-ray, will realize a lower refractive index and bend at a lower angle. The ray is called the extraordinary ray or E-ray.
Difference between O-ray & E-ray
|
SL No.
|
O-ray
|
E-ray
|
|
01
|
O-ray obey Snail’s law of reflection.
|
E-ray does not obey Snail’s law of reflection.
|
|
02
|
Velocity of O-ray is same for all direction.
|
Velocity of E-ray is different for different direction. |
|
03
|
For O-ray wavefront is spherical.
|
For O-ray wavefront is spherical. |
Refractive index
The index of refraction or refractive index is a ratio of the velocity of light in a vacuum to the velocity of light in the medium.
Velocity of light in vacuum ∴ Refractive index (n)= ————————————————— Velocity of light in the medium
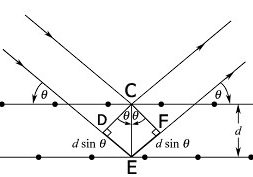
Snell’s law is related to the index of refraction
VA sinθA nB
Snell's law = —— = ——— = ——
VB sinθB nA
Where
VA & VB = the speed of light in two mediums
nA & nB = the refractive index of two the mediums
θA =the angle of incidence
θB =the angle of incidence
Relation among refractive index, density and swelling
The refractive index of fibers is affected by the fiber density. For many fibers, the relationship between refractive index and fiber density (r) can expressed by Gladstone and Dale’s law:
n-1 ——=Constant η
If the average reflective index is used, the value of constant is 0.3570.
A similar relationship can be obtained between refractive index (nm) and volume vm of a mixture of different components.
Vm(nm-1) = v1(n1-1) + v2(n2-1) + v3(n3-1) +… … … …
Where v1, v2, v3, … and n1, n2, n3, … are the reflective indices and volumes of the individual components. The refractive index of water is 1.333. So that, the effect of moisture on the refractive index can be described by:
vMR(nMR-1) = v0(n0-1) + 0.333MR
Where,
v0=volume of 1 gm of dry fiber
vMR =volume of the sample fiber at a frictional moisture regain of MR
n0 & nMR =refractive index of dry and moisture fiber respectively
The equation applies to the refractive index nιι & n⊥ and we find how the birefringence varies with the moisture vs swelling of the fibers:
vMR( nιι – n⊥)MR = V0( nιι – n⊥)
How does the fiber density affect the refractive index of a fiber?
The refractive index of fibers is affected by the fiber density. This is because, the refractive index will increase when the number of molecules present increase. For many fibers, the relation between refractive index and fiber density (ρ) can be expressed by Gladstone and Dale’s law:
n-1 ——=Constant η
Effect of moisture regain on the refractive index of fiber?
The refractive index of water is 1.33. The refractive index values of most fibers are greater than of water, and hence they decrease with increase in moisture regain. Figure shows schematically the effect of moisture on the average refractive index of fibers. For some fibers, an increase in refractive index is observed at low moisture regains and this probably is caused by the filling up of voids or defects in the fibers by water.
Effect of moisture on the refractive index can be described by:
vMR(nMR-1) = v0(n0-1) + 0.333MR
Where,
v0 = volume of 1 gm of dry fiber
vMR = volume of sample fiber at a frictional moisture reign of MR
n0 = refractive index of dry fiber
nMR= refractive index of moisture fiber
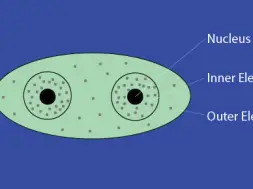
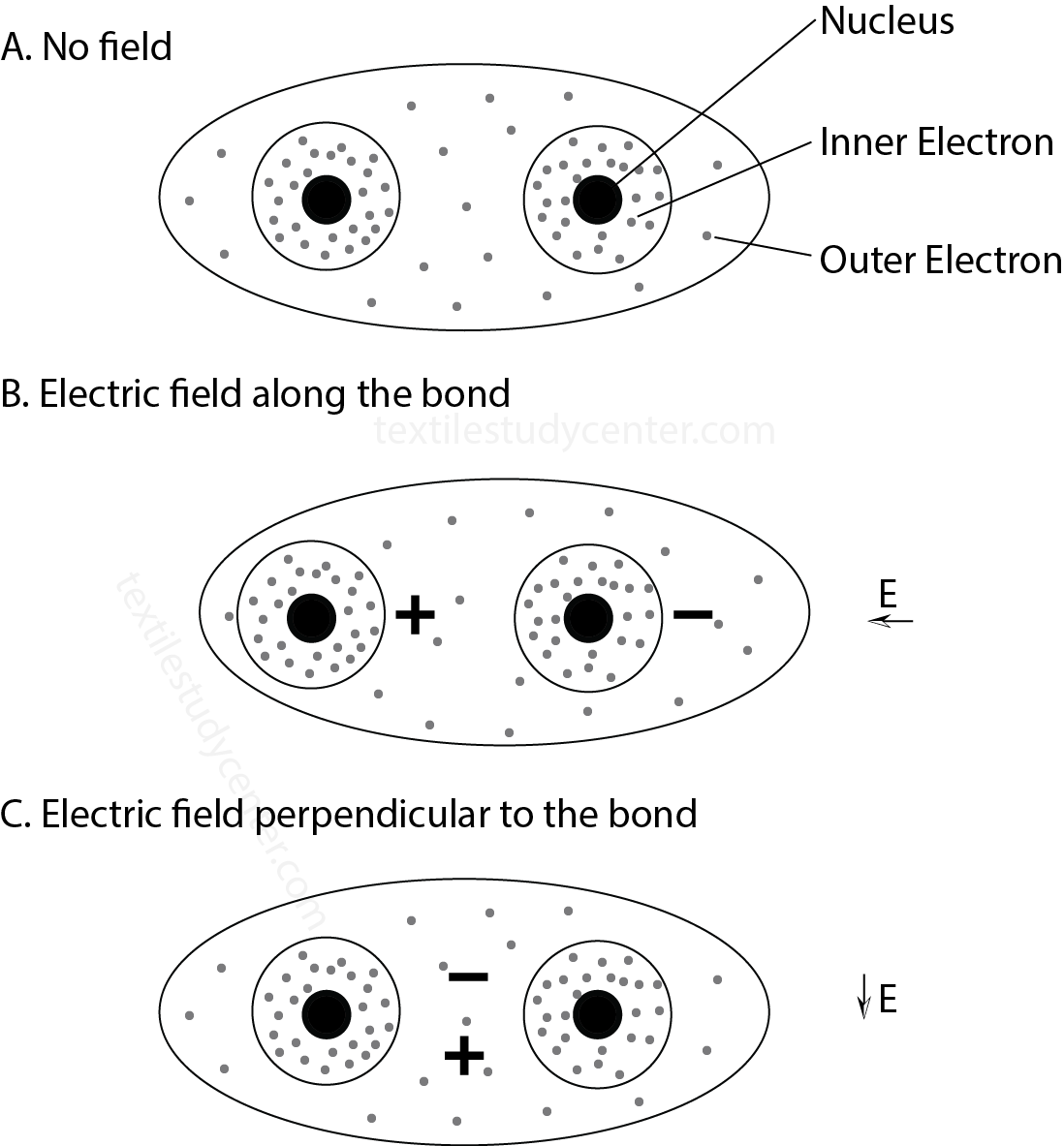
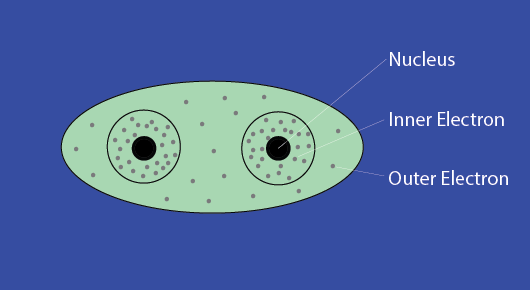
Electronic polarization on fiber atoms
When light is transmitted through a fiber, the polarisability is varied with the direction of electric field. In general the election in the inner shells are not easily displaced. Hence only the outer electrons, which involved in the covalent bonds, are effected by light weaves. The electronic is the greatest when the electric field is applied along the direction of a covalent bond.
In isotropic materials, the covalent bonds are arranged randomly in all directions, so that the refractive index is the same in all directions.
And in anisotropic materials, such as textile fibers, the molecules are linked up in certain preferred direction. As a result, refractive index varies with the direction of the electric field.
(3279)
Md Sohanur Rahman Sobuj
Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018
