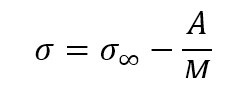
Mechanical Properties of Polymers
Mechanical Properties of Polymers
Mechanical Properties:
It is of great importance to be familiar with some basic mechanical properties of the material before its application in any field, such as how much it can be stretched, how much it can be bent, how hard or soft it is, how it behaves on the application of repeated load and so on.
A . Strength: In simple words, the strength is the stress required to break the sample. There are several types of the strength, namely tensile (stretching of the polymer), compressional (compressing the polymer), flexural (bending of the polymer), torsional (twisting of the polymer), impact (hammering) and so on.
The polymers follow the following order of increasing strength:
linear < branched < cross-linked < Network.
Factors Affecting the Strength of Polymers:
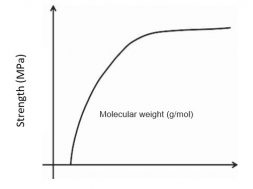
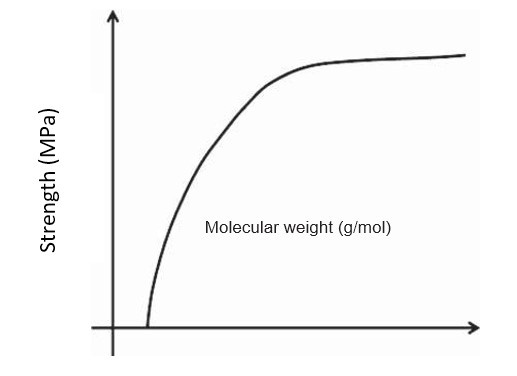
- Molecular Weight: The tensile strength of the polymer rises with increase in molecular weight and reaches the saturation level at some value of the molecular weight (Fig. 1). The tensile strength is related to molecular weight by the following equation.
σ∞ is the tensile strength of the polymer with molecular weight of infinity. A is some constant, and M is the molecular weight. At lower molecular weight, the polymer chains are loosely bonded by weak van der Waals forces and the chains can move easily, responsible for low strength, although crystallinity is present. In case of large molecular weight polymer, the chains become large and hence are entangled, giving strength to the polymer.
- Cross-linking: The cross-linking restricts the motion of the chains and increases the strength of the polymer.
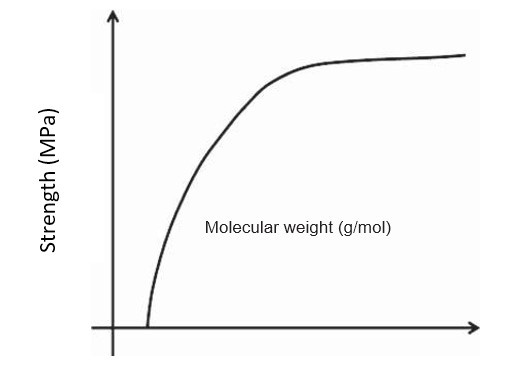 Fig1.Variation of tensile strength with molecular weight of the polymer.
Fig1.Variation of tensile strength with molecular weight of the polymer.
- Crystallinity: The crystallinity of the polymer increases strength, because in the crystalline phase, the intermolecular bonding is more significant. Hence, the polymer deformation can result in the higher strength leading to oriented chains.
B . Percent Elongation to Break (Ultimate Elongation): It is the strain in the material on its breakage, as shown in Fig. A1.10. It measures the percentage change in the length of the material before fracture. It is a measure of ductility. Ceramics have very low (<1%), metals have moderate (1–50%) and thermoplastic (>100%), thermosets (<5%) value of elongation to break.
C . Young’s Modulus (Modulus of Elasticity or Tensile Modulus): Young’s Modulus is the ratio of stress to the strain in the linearly elastic region (Fig. A1.11). Elastic modulus is a measure of the stiffness of the material.
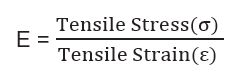
D . Toughness: The toughness of a material is given by the area under a stress–strain curve
Toughness = ∫ σ dε
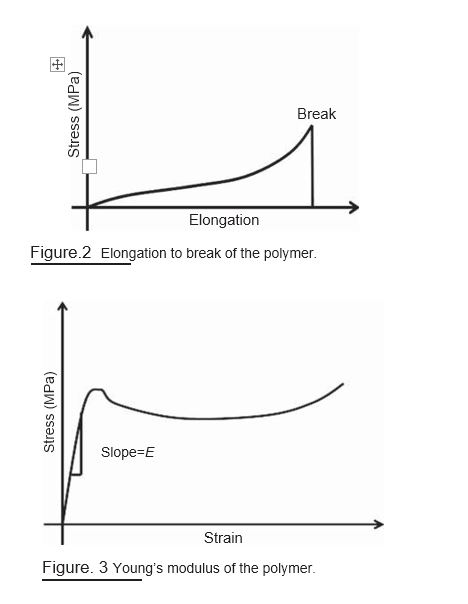
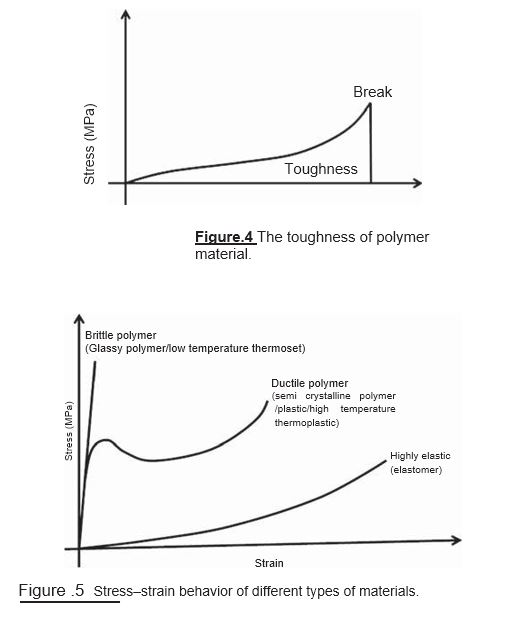
The toughness measures the energy absorbed by the material before it breaks. A typical stress–strain curve is shown in Fig. 5, which compares the stress–strain behavior of different types of materials. The rigid materials possess high Young’s modulus (such as brittle polymers), and ductile polymers also possess similar elastic modulus, but with higher fracture toughness. However,elastomers have low values of Young’s modulus and are rubbery in nature.
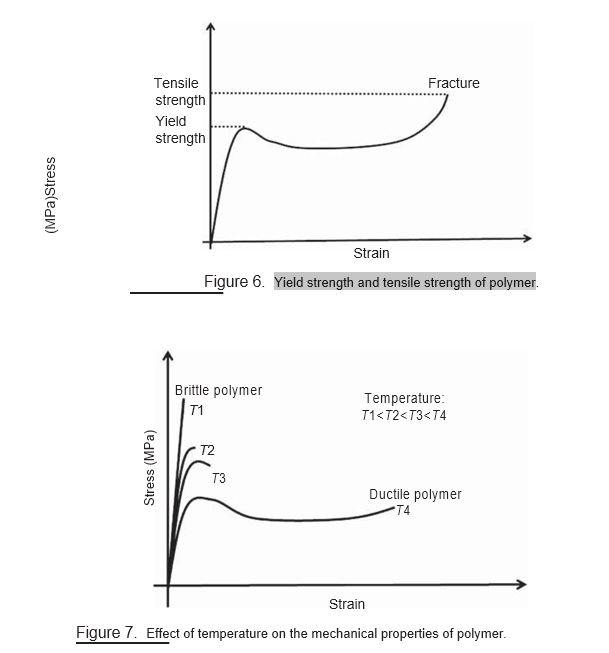
The yield strength of the plastic polymer is the corresponding stress where the elastic region (linear portion of the curve) ends (Fig. 6). The tensile strength is the stress corresponding to the fracture of the polymer. The tensile strength may be higher or lower than the yield strength (Fig. 6).
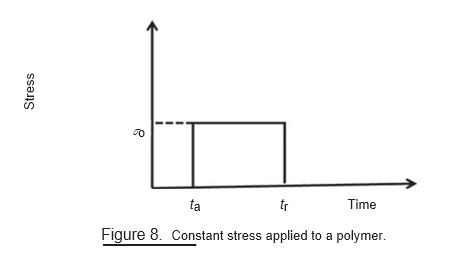
The mechanical properties of the polymer are strongly affected by the temperature. A typical plot of stress versus strain is shown in Fig. 7. From the plot, it is clear that with increase in the temperature, the elastic modulus and tensile strength are decreased, but the ductility is enhanced.
E . Visco-elasticity: There are two types of deformations: elastic and viscous. Consider the constant stress level applied to a material as shown in the Fig. 8. In the elastic deformation (Fig. 9), the strain is generated at the moment the constant load (or stress) is applied, and this strain is maintained until the stress.
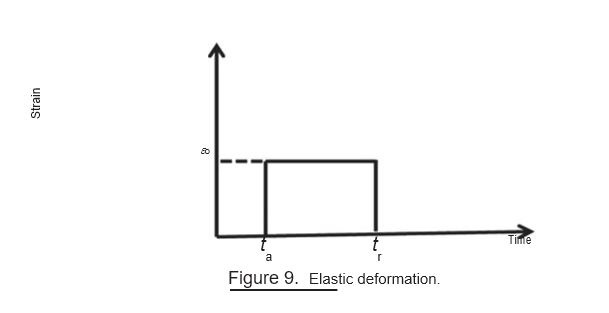
is not released. On removal of the stress, the material recovers its original dimen-sions completely, that is the deformation is reversible (Fig. 9), that is:
σ= Eε
where E is the elastic modulus, is applied stress, and is the strain developed.
However, in viscous deformation (Fig. A1.18), the strain generated is not instanta-neous and it is time dependent. The strain keeps on increasing with time on application of the constant load, that is, the recovery process is delayed. When the load is removed, the material does not return to its original dimensions completely, that is, this deformation is irreversible (Fig. 10).
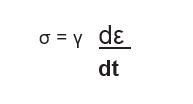
where, ү= viscosity, and
d ε/dt = strain rate
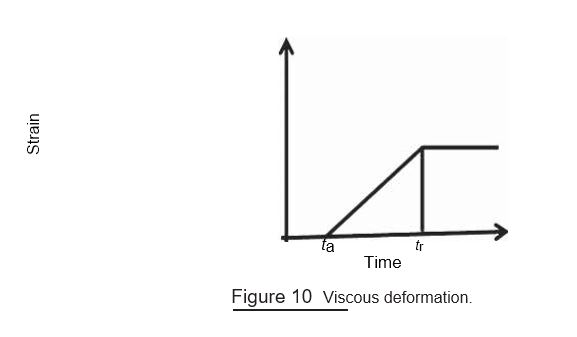
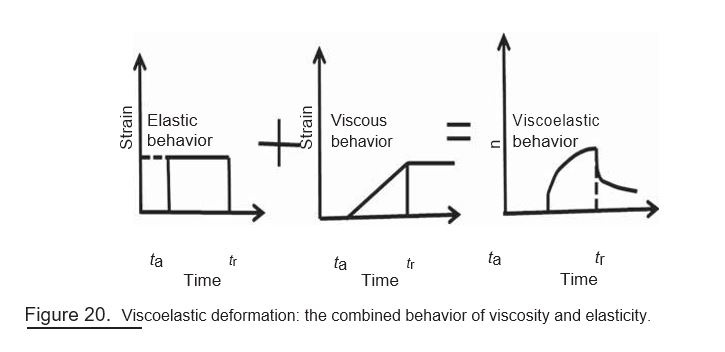
Usually, polymers show a combined behavior of elastic and plastic deformation (Fig. 20) depending on the temperature and strain rate. At low temperature and high strain rate, elastic behavior is observed, and at high temperature but low strain rate, the viscous behavior is observed. The combined behavior of viscosity and elasticity is observed at intermediate temperature and strain rate values. This behavior is termed as viscoelasticity, and the polymer is termed as viscoelastic.
Viscoelastic Relaxation Modulus. At a given temperature, when the polymer is strained to a given value, then the stress required to maintain this strain is found to decrease with time. This is called stress relaxation (Fig. 21). The stress required to maintain the constant strain value is decreased with time, because the molecules of polymer get relaxed with time, and to maintain the level of strain, somewhat lower value of stress is sufficient (Fig. 21).
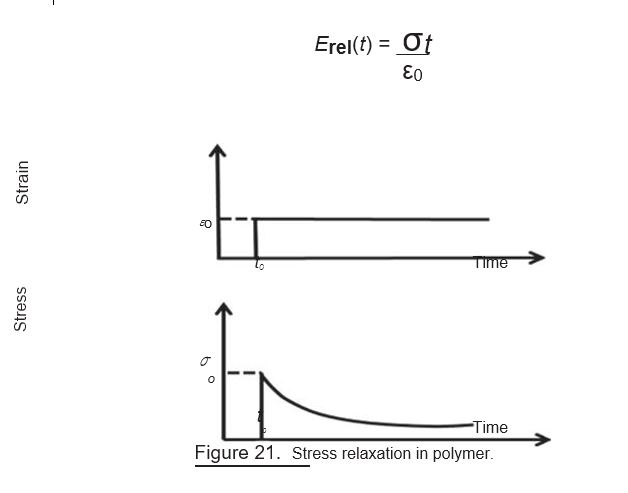
The decrease in stress follows the exponential decay:
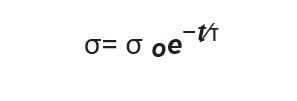
where
σ= stress at time t,
σo = peak stress level, and
τ= relaxation time constant.
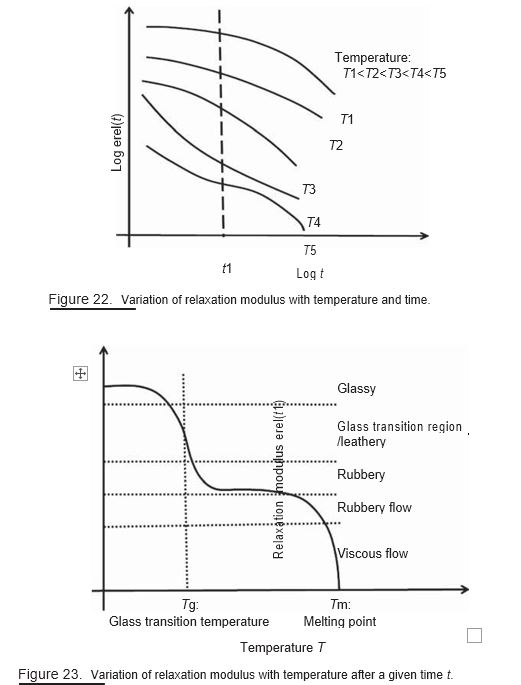
The relaxation modulus is found to decrease with increase in temperature and time as shown in Fig. 22
Now, consider the time t1. Measure the values of relaxation modulus at time t1 at different temperatures, say T1, T2, T3 … for the viscoelastic polymer and plot the relaxation modulus versus temperature. A typical plot is shown in Fig. 23 The glass transition temperature lies near the upper temperature extremity.
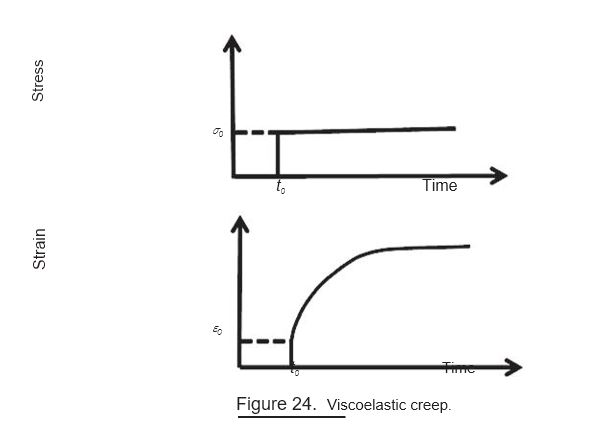
Viscoelastic Creep: creep can be considered as the opposite of stress relaxation (lowering of the stress with time maintaining the constant strain level) where the poly-mer suffers time-dependent deformation (increasing strain with time) at constant stress level. At a given temperature, when a constant load is applied to the material, there is a time-dependent increase of strain in the material (Fig. 24). This behavior of the material is called viscoelastic creep. The increase in molecular weight and stiffness of the chains results in better creep resistance of the material.
We can define the time-dependent creep modulus as follows:

where
σo = constant applied stress,
ε(t) = strain at time t.
(523)