Tensile Testing Terms and Tensile Testing Terms Definitions
Md Sohanur Rahman Sobuj
Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018
Tensile Testing Terms and Tensile Testing Terms Definitions
Engineering stress: Engineering stress can be equated to the load applied per original cross sectional area.
True stress: True stress can be equated to the load applied per instantaneous (actual) cross sectional area.
Unit: N/m2 (Pa)
Mass/Specific stress: The ratio between applied load and linear density (mass per unit length or count number) is called specific stress. Specific stress is dimensionally equivalent to energy per unit mass, which is relevant to some application. N/tex equals kJ/g.
Unit: N /(kg/m), N/tex (1 N/tex=106 N m/kg)
Relation between stress, specific stress and density
Stress: Stress can be equated to the load applied per original cross sectional area.
Specific stress: The ratio between applied load and linear density (mass per unit length or count number) is called specific stress.
Why specific stress is important in textile materials?
Specific stress is a useful parameter to describe the fiber cross-sectional fineness. In textile materials, conventional stress (force per unit area) is very difficult to practically estimate the cross-sectional dimensions. Besides, specific stress (force per unit linear density) is more useful for fibers and is the usual mode in the textile community.
Tensile stain: Due to stress, the ratio of elongation to initial specimen length is known as “stain”. They have no unit.
Math: Find the specific stress of a fiber with mass, Length, under a load of 0.3 N.
Math: Find the stress for a cotton fiber with mass m=0.35g, length =1.5 cm under a load of 0.015N. Given the density, for cotton.
Breaking load/force: The load at which the material break is called breaking load. It is usually expressed in gm-wt or lb-wt
Breaking length: The length of the specimen which will just break under its own wt. when hung vertically is called breaking length. Breaking length is an older measure of tenacity. It is usually measured in kilometers.
E.g. 10 tex yarn breaks at a load of 150 grams
∴The numerical value is equal to tenacity in g/tex (150/10)
Breaking length would be = 15 km
Breaking extension: The extension to break the material to the initial length of that material is known as breaking extension. It is expressed as %.
Breaking strength /Tensile strength: Force applied to break the fibers to cross-sectional area is known as breaking strength/tensile strength.
Unit: N/m2, dyne/cm2
In between, nylon and polyester, which one has more breaking force?
Breaking force is related to the diameter of the fiber. Breaking force is proportional to the diameter of the fiber.
We know that,
Diameter of nylon>diameter of polyester
So, nylon has more breaking force than polyester.
Tenacity: The ratio of load required to break the specimen and the linear density (count of that yarn) of that specimen is called tenacity.
Unit: gm/denier, gm/Tex, N/Tex, CN/Tex etc.
Math:Calculate the tenacity of 60 D nylon fiber when it breaks at 400 gm force and 50 cm length.
Yield point: In which point of stress-strain point curve, the yarn tends to yield on a further increase in stress and produce a relatively large extension for small stress is called yield point. The values of stress and strain at the yield point are known as yield stress and yield strain, respectively.
Since the stress–strain curve is approximately linear up to the yield point, the work to the yield point will be almost equal to ½ ( yield stress ×yield strain)
Yield stress: The stress at yield point is called yield stress.
Yield strains: The strain at yield point is called yield strain.
Yield strength: The stress at which material strain changes from elastic deformation to plastic deformation, causing it to deform permanently.
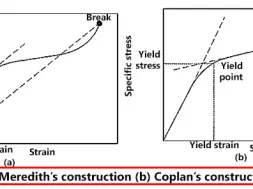
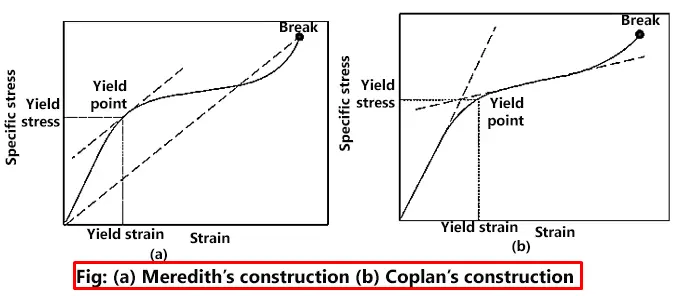
Two theories of yield point construction
Meredith yield point: According to Meredith, the point at which the tangent to the curve is parallel to the line joining the origin and the breaking point is taken as the yield point, [Fig. (a)].
Coplan yield point: According to Coplan method, the yield point occurs at the stress given by the intersection of the tangent at the origin with the tangent having the least slope, as shown in Fig. (b)
Initial modulus or stiffness: Fiber stiffness is commonly determined by the initial slope of the stress-strain curve at the origin. This is commonly known as the initial modulus; the higher initial modulus, the stiffer the fiber and the lower initial modulus, the more flexible the fiber.
Tan α ↑ → extension ↓
The effect of initial modulus in textiles:
Orientation: For higher orientation fiber, higher initial modulus.
Crystallinity: For higher Crystallinity fiber, higher initial modulus.
Extensibility: For lower extensibility of fiber, higher initial modulus.
Stiffness: For lower stiffness of fiber, higher initial modulus.
Chemical structure: High ring structure of molecular chain in fiber, higher initial length.
Elastic and plastic behavior of textile fiber
Elasticity or Elastic recovery is a property of material to tend to recover original size and shape after deformation. When a material is allowed to recover from its maximal deformation, the part of the total deformation which is recoverable is called elastic, and the other part that is non recoverable is called plastic, as shown in Fig.
Here, OA = initial length of the specimen
OA= final length after recovery
BC = elastic extension
AB= plastic extension
Total extension = Elastic extension + Plastic extension
Total work = work required for elastic extension + work required for plastic extension
Internal change due to elastic and plastic deformation
In the initial stage of S-S curve, the elongation is mainly due to the amorphous regions in which primary (inter-atomic) and secondary bonds (inter-molecular) are stretched and sheared (Fig. a and b). If the stretch is removed at this stage, the most extension will be recovered and the material would exhibit elastic properties.
By increasing the stress further, the S-S curve bends sharply at yield point where a significant number of secondary bonds break. Alter that cold-drawing starts with necking where large strains are produced by a small increase in stress, called natural drawing resign. A sort of plastic deformation of the materials occurs here. The long-chain molecules orient themselves with further breaking of secondary bonds. This orientation of the molecules leads the material in a better position to resist further stress and then the rate of extension decreases. This phenomenon is known as ‘stain hardening’ by which the material gains modulus and strength because of stain –induced recrystallization (Fig.c)
Stain hardening: Stain hardening is a process in which a fiber is permanently deformed in order to increase its resistance to further deformation or Some materials show increased stress during plastic flow, with a phenomenon called strain hardening.
Work recovery: The ratio between work returned during recovery and total work done in total extension is called work recovery.
(4619)
Md Sohanur Rahman Sobuj
Latest posts by Md Sohanur Rahman Sobuj (see all)
- Thermal Properties of Polymers - April 26, 2019
- Frictional Properties - September 15, 2018
- Torsional Properties of Textile Materials - August 30, 2018
